In today’s information-explosion world, we are constantly bombarded with claims made by individuals, organizations, and companies. Advertisers emphasize the quality of their products, universities boast about the salaries of their graduates, and pharmaceutical companies promote the efficacy of their medicines. But how do we know if these claims are trustworthy? Hypothesis testing offers a systematic approach to assess the validity of such claims.
Although hypothesis testing might seem complicated, the core concept is straightforward: it helps to determine whether there is sufficient evidence to support a specific claim or hypothesis. In this blog post, i will explain what hypothesis testing is and how it works.
Introduction to Hypothesis Testing
Let’s start with a real-world example. Tesla, the electric vehicle company, claims that their Model S sedan has a mean range of 359 miles between charges (Tesla website). How could we verify this claim? One approach is to study a random sample of 100 Model S cars and calculate their average range. If Tesla’s claim is accurate, we would expect the sample mean to be close to 359 miles. If the claim is false, the sample mean would likely be significantly lower than the advertised figure, assuming advertisers usually claim their best results.
The critical question is: what constitutes “significantly lower”? In the Tesla example, if the sample mean range is only 150 miles, we would have strong reason to doubt the claim. In contrast, if the sample mean is 360 miles, it would provide strong evidence supporting the claim. But how do we deal with less obvious cases? For instance, if the sample mean is 334 miles, should we consider that “significantly lower” than the claimed mean range of 359 miles?
In statistics, hypothesis testing is the standard procedure used to answer such questions. For our Tesla example, with the sample mean of 334 miles from the randomly selected samples, the process would work as follows:
- We start by assuming that the advertised claim is true, meaning the mean range of the population of all Tesla Model S sedans equals to 359 miles.
- Using this assumption, we calculate the likelihood of drawing a random sample where the sample mean deviates from 359 miles by at least as much as the one we found. Specifically, we calculate the likelihood of drawing another random sample (of size 100) with a sample mean of 334 miles or less.
- If such a sample is fairly likely to have occurred by chance, we have evidence that the claim might be true. However, if the sample is unlikely to have occurred by chance, we have reason to believe the population mean range is probably not what the advertisement claims.
Please note that even if a sample result is very likely to have occurred by chance, this does not prove the claim is true; it only suggests the claim might be valid. There could still be other explanations for the sample result, such as an unusual sample selection or confounding variables that were not accounted for.
Now, let’s define hypothesis testing more precisely. In statistics, a hypothesis is a claim about a population parameter. In the Tesla example, the population parameter is the mean range between charges. Hypothesis testing is a method to determine whether a particular claim about a population parameter is supported by available sample evidence.
Hypothesis Testing Process
Hypothesis testing is a structured process to evaluate claims or ideas based on sample evidence. Here’s an outline of the general process, followed by an explanation of the key concepts.
Step 1: Formulate the hypotheses:
- Null Hypothesis ($H_0$): the initial assumption for a hypothesis testing, usually claiming a specific value for a population parameter.
- Alternative Hypothesis ($H_a$) : claiming the population parameter differs from the value specified in the null hypothesis.
Step 2: Set a Significance Level ($\alpha$)
The significance level represents the probability of rejecting the null hypothesis when it is actually true (Type I error, which will be explained later). Common significance levels are 0.05 (5%) or 0.01(1%).
Step 3: Collect Sample Data
Draw a sample from the population and measure the relevant sample statistics, such as sample size($n$), sample mean($\overline{x}$) or sample proportion($\hat{p}$).
Step 4: Calculate P-Value
Assuming the null hypothesis is true, calculate the probability of observing a sample statistic (mean or proportion) at least as extreme as the one you found. This probability is known as the the P-value.
Step 5: Make a Decision
Compare the P-value to the chosen significance level:
- If the P-value is less than the significance level, reject the null hypothesis.
- If the P-value is greater than or equal to the significance level, fail to reject the null hypothesis.
Let’s walk through some of the key concepts in the hypothesis testing process.
Formulating Hypotheses
In any hypothesis test, we consider at least two hypotheses:
- Null Hypothesis ($H_0$): usually assumes “no effect”, “no difference”, or “equals to”, making it a statement that the population parameter equals to a specific value.
- Alternative Hypothesis ($H_a$): usually a statement that contradicts the null hypothesis. With the null hypothesis in the form of equality, the alternative hypothesis may take one of the three forms:
- Left-tailed test: population parameter < claimed value
- Right-tailed test: population parameter > claimed value
- Two-tailed test: population parameter ${=}\llap{/\,}$ claimed value
The null and alternative hypotheses should aways be formulated before drawing a sample from the population for testing.
For our Tesla example, the hypotheses can be formulated as follows:
- Null Hypothesis ($H_0$): the mean range of Model S = 359 miles
- Alternative Hypothesis ($H_a$): the mean range of Model S < 359 miles
Significance Level ($\alpha$)
It is crucial to decide on the level of significance before conducting a hypothesis test. Depending on the situation, a higher or lower level of significance may be appropriate. You can think of significance level as a “risk tolerance” to the probability of making a type I error - rejecting the null hypothesis while actually it is true.
In a statistical studies, a result is said to be statistically significant if it is unlikely to have occurred by chance. To quantify the idea, we use a probability to measure the likelihood that a result occurred by chance. For example, if the probability that the observed result occurred by chance is less than or equal to 0.05 (5% or 1 in 20), we say the result is statistically significant at the 0.05 level. If not, the observed difference is reasonably likely to have occurred by chance, so we say the result is not statistically significant at the 0.05 level.
While the 0.05 level is commonly used, other significance levels, such as 0.01 (1%) and 0.001 (0.1%), may be chosen depending on the context. A lower α means a lower risk tolerance, requiring stronger evidence to reject the null hypothesis.
P-Value
We will discuss the calculation of P-Values for hypothesis tests in other posts. Here we focus on the interpretation.
The P-Value is a critical component of hypothesis testing. It represents the probability of selecting a sample with a sample statistic as extreme or more extreme as the one obtained, assuming that the null hypothesis is true.
- A small P-value (e.g., < significance level, such as 0.05 or 0.01) indicates that the sample result is unlikely and provides a good reason to reject the null hypothesis.
- A larger P-value suggests that the sample results might have occurred by chance, leading to a failure to reject the null hypothesis.
To remember the rule: “if the P-value is low, the null must go.”
Outcomes of a Hypothesis Test
Hypothesis testing always begins with the assumption that the null hypothesis is true. We then test to see if the data give us reason to think otherwise. As a result, there are only two possible outcomes to a hypothesis test:
- Reject the null hypothesis
- Fail to reject the null hypothesis
It is important to note that “accepting the null hypothesis” is not a possible outcome, because the null hypothesis is always the initial assumption. The test may not provide sufficient evidence to reject this assumption, but it cannot, by itself, prove that the assumption is true. Therefore, we never conclude that there is sufficient evidence to support a null hypothesis.
The idea that a hypothesis test cannot lead us to accept the null hypothesis illustrates the adage “absence of evidence is not evidence of absence.” This concept also explains why it is easy to claim the existence of mythical creatures, such as Bigfoot or the Loch Ness Monster, while disproval of their existence is nearly impossible.
Type I Error, Type II Error, and Statistical Power
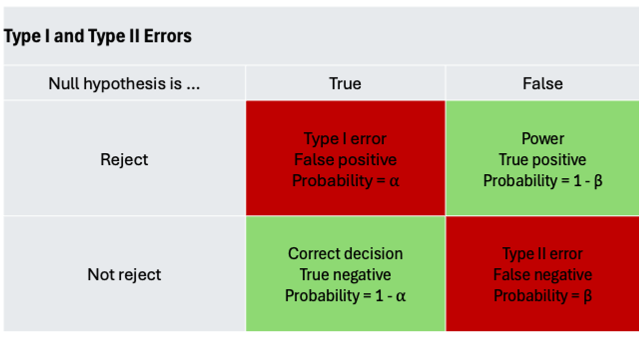
Even when hypothesis testing is conducted correctly, two common types of errors may still occur. In the Tesla example, where we are testing the claim that the mean range of Model S sedans is 359 miles, two possible incorrect conclusions can be made:
- Type I Error (False Positive, $\alpha$): occurs when we wrongly reject the null hypothesis when it is true.
- Type II Error (False Negative, $\beta$): occurs when we fail to reject the null hypothesis when it is false.
The significance level of a hypothesis test corresponds to the probability of making a Type I Error. For example, if we conduct the Tesla hypothesis test at a 0.05 significance level, there is a 0.05 (5%) probability that we might make the mistake of rejecting the null hypothesis when it is actually true.
Additionally, Statistical Power (1 - $\beta$) is the probability that a test correctly rejects the null hypothesis when it is false. Higher power means a better chance to detect false claims.
A Legal Analogy
A legal analogy could help clarify these key concepts of hypothesis testing. In the United States, a fundamental principle in courtroom trials is that a defendant is presumed innocent until proven guilty beyond a reasonable doubt. The starting assumption of innocence represents the hypotheses:
- $H_0$: the defendant is innocent
- $H_a$: the defendant is guilty
The prosecutor’s role is to present evidence that persuades the jury to reject the null hypothesis. If the persecutor fails to provide sufficient evidence, the jury will not reject the null hypothesis. However, finding a person innocent (or accepting the $H_0$) is not an option: a verdict of not guilty means the evidence is insufficient to establish guilt, but it does not prove innocence.
Different cases need different standards of reasonable doubt. For example, a civil case involving a $5000 fine might require a less strict standard, thus higher level of significance, than a criminal case involving a death penalty, where the consequences of wrongly rejecting the null hypothesis are severe.
The following table summarizes the major factors of hypothesis testing and their corresponding courtroom trial concepts.
| Concepts | Hypothesis Testing | Courtroom Trial |
|---|---|---|
| Null Hypothesis ($H_0$) | Equals the claimed value | The defendant is innocent |
| Alternative Hypothesis ($H_a$) | Not equals the claimed value | The defendant is guilty |
| Significance level ($\alpha$) | A “risk tolerance” of making a Type I error | The “reasonable doubt” standard |
| P-value | Probability of observing a sample statistic as extreme or more extreme, assuming $H_0$ is true | The strength of the prosecutor’s evidence (a lower P-value means stronger evidence against innocence) |
| Type I Error | Rejecting the null hypothesis when it’s true | Wrongly convicting an innocent defendant |
| Type II Error | Failing to reject the null hypothesis when it’s false | Acquitting a guilty person |
| Statistical Power (1- $\beta$) | Probability of correctly rejecting the $H_0$ when it’s false. | Ability to correctly convict a guilty person |
Conclusion
Hypothesis testing, though might seem intimidating at first, is a powerful tool for evaluating claims based on evidence. By understanding its basic principles, you can appreciate its role in scientific research and everyday decision-making.
I hope this post has clarified what a hypothesis is and how hypothesis testing works. Thanks for reading and looking forward to your comments.