Constraints Programming (CP) is a relatively new, but evolving rapidly, paradigm in Operation Research. It was derived from Computer Science - Logic Programming, Graph Theory, and Artificial Intelligence. Like a Mathematical Programming (MP), such as Linear Programming, Integer Programming, or Nonlinear Program, CP works with the same concepts of decision variables, constraints, and/or objective function. Because of its flexible modeling language and powerful search strategy, CP is a powerful and easy-to-use optimization technology to solve highly combinatorial optimization problems, such as scheduling problems, timetabling problems, sequencing problems, and allocation or rostering problems. These problems might be difficult to solve for traditional MP, due to: 1) constraints that are nonlinear in nature; 2) a con-convex solution space that contains many locally optimal solutions; 3) multiple disjunctions, which result in poor information returned by a linear relaxation of the problem. This post tries to summarize some major benefits of CP in contrast with MP models in modeling and solving standpoints.
Intuitive Modeling Language
Comparing to MP, CP allows more flexible modeling language, which is more intuitive and closer to natural language. Virtually any expression over the variables is allowed.
1. Wide Types of Decision Variables
The decision variable types in CP include the classical binary, integer, and continuous. Unlike in Integer Programming, where the range of a variable is specified and maintained as an interval, in CP the variables are maintained explicitly as a set of elements that is called domain. In addition, CP can model special “structured” variable types. One example of this special variable types is the set variables that take a set of elements as value. Another example is activities or interval variables that are suitable to model the scheduling and sequence problem.
2. Nearly All Kinds of Constraints Expressions
With the explicit element representation, CP allows wider types of constraints to be defined by arbitrary expressions through algebraic or logical operators. Specially, logical constraints, such as AND, OR, NOT and IF-THEN, and ’global constraints’, such as FORALL, EXISTS, SUM, ALLDIFFERENT can be easily formulated in CP. Here are some example expressions:
Arithmetic Expressions: \(x^2 \cdot (y^2 - z) \ge 25 + x^2 \cdot \max(x,y,z)\)
Extensional Constraints(‘Table’ Constraints): \((x, y, z) in MyTupleSet\)
Variables as Subscripts (‘Element’ Constraints): \( y = cost(x) \), where y and x are variables, ‘cost’ is an array of parameters.
Reasoning with meta-constraints: \(\sum_{\substack{0\le i \le m}}(x_i \gt T_i) \ge 5 \)
Logical rations in which (meta-) constraints can be mixed: \( (x \lt y) \vert (y \lt z) \rightarrow c = \min(x, y) \)
Global Constraints: \( Alldifferent(x_1, x_2, …, x_n) \)
In general, CP contraints can be non-linear, non-differentiable, and discontinuous.
3. With or Without Objective Function
Depending on with or without an objective function, constraint programming models can be categorized into two types: constraint optimization problem (COP) with an objective function and constraint satisfaction problem (CSP) without an objective function. COP aims to find an optimal solution, while CSP can provide a feasible solution or proves that no solution exists.
Powerful Search Strategy
The solving process underlying CP involves a systematic search over a search space. Initially, the search space contains all combinations of the values in the domains of all decision variables. To avoid exploring the entire search space, CP first removes inconsistent values from the domains of the variables involved in each constraint. Then a search strategy (depth first, width first or multi-start) is applied to guide the search for a solution within the reduced search space. The search process can be viewed as traversing a tree, where the root is the starting point, a leaf node is a combination of values in the reduced search space and each branch represents a move (branching) within the search. Each leaf node is evaluated to determine if it will produce a feasible solution. A solution is a set of value assignments to the decision variables such that each variable is assigned to exactly one value from its domain.
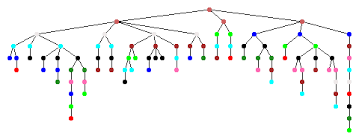
Combination With Other Solution Framework
Constraint programming can also be used as a fast generator of feasible solutions. This can be extremely useful in combination with other models and engines, for instance to implement column generation for a complex optimization model.
References
-
Willem-Jan van Hoeve. Introduction to Constraint Programming and Operations Research Techniques in Constraint Programming. ACP Summer School on Constraint Programming, 2012.